Daesung Kim and Hye Won Chung
IEEE Transactions on Information Theory
We consider a query-based data acquisition problem for binary classification of unknown labels, which has diverse applications in communications, crowdsourcing, recommender systems and active learning. To ensure reliable recovery of unknown labels with as few number of queries as possible, we consider an effective query type that asks “group attribute” of a chosen subset of objects. In particular, we consider the problem of classifying m binary labels with XOR queries that ask whether the number of objects having a given attribute in the chosen subset of size d is even or odd. The subset size d, which we call query degree, can be varying over queries. We consider a general noise model where the accuracy of answers on queries changes depending both on the worker (the data provider) and query degree d. For this general model, we characterize the information-theoretic limit on the optimal number of queries to reliably recover m labels in terms of a given combination of degree-d queries and noise parameters. Further, we propose an efficient inference algorithm that achieves this limit even when the noise parameters are unknown.
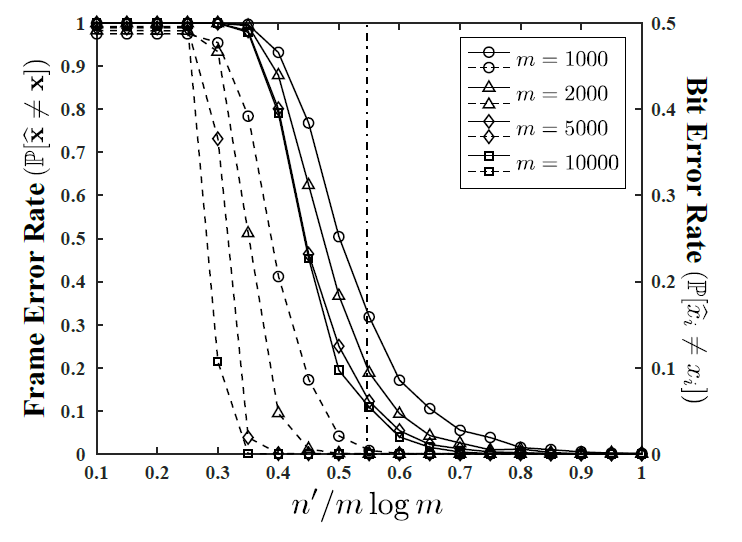
Figure 1. Frame error rate, and bit error rate of the proposed algorithm vs. number of queries for four different values of m.