Author: Daesung Kim and Hye Won Chung
Keywords: Crowdsourcing, XOR Queries, Fundamental Limits, Inference
Abstract:
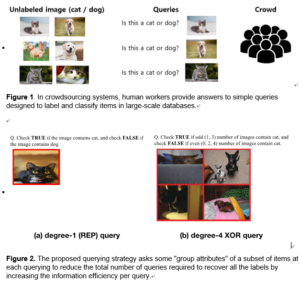
We consider a query-based data acquisition problem for binary classification of unknown labels, which has diverse applications in communications, crowdsourcing, recommender systems and active learning. To ensure reliable recovery of unknown labels with as few queries as possible, we consider an effective query type that asks “group attribute” of a chosen subset of objects. In particular, we consider the problem of classifying m binary labels with XOR queries that ask whether the number of objects having a given attribute in the chosen subset of size d is even or odd. The subset size d, which we call query degree, can be varying over queries. We consider a general noise model where the accuracy of answers on queries changes depending both on the worker (the data provider) and query degree d. For this general model, we characterize the information-theoretic limit on the optimal number of queries to reliably recover m labels in terms of a given combination of degree-d queries and noise parameters. Further, we propose an efficient inference algorithm that achieves this limit even when the noise parameters are unknown.
이 논문에서는 알려지지 않은 이진 레이블을 쿼리를 통해 복구하는 문제를 연구한다. 이진 레이블의 분류는 통신 시스템, 크라우드소싱, 추천 시스템, 능동 학습 등 다양한 분야에서 활용되는 중요한 문제이다. 최대한 적은 수의 쿼리를 통해 레이블을 복구하기 위하여 어떤 레이블의 묶음에 대한 질문을 하는 방식을 제안하였다. 구체적으로는 총 m개의 이진 레이블 중 특정 d개를 선택하여 이들의 XOR값을 묻는 방식을 사용하였다. 여기서 d는 “쿼리 난도”로 정의되며, 매 쿼리마다 변할 수 있도록 설정되었다. 또한, 쿼리의 정답률이 대답하는 사람과 쿼리 난도 두 가지 모두에 의해 결정되는 일반적인 모델을 가정하였다. 이러한 설정에서 모든 레이블을 복구하기 위해 필요한 쿼리의 개수를 이론적으로 계산하였다. 여기에 더하여 대답하는 사람들의 정확도를 모르는 상황에서도 앞에서 계산한 이상적인 쿼리 개수만을 사용하여 모든 레이블을 복구해내는 알고리즘을 제안하였다.