[Title]
Feedback Gradient Descent: Efficient and Stable Optimization with Orthogonality for DNNs
[Authors]
Fanchen Bu, Dong Eui Chang
[Abstract]
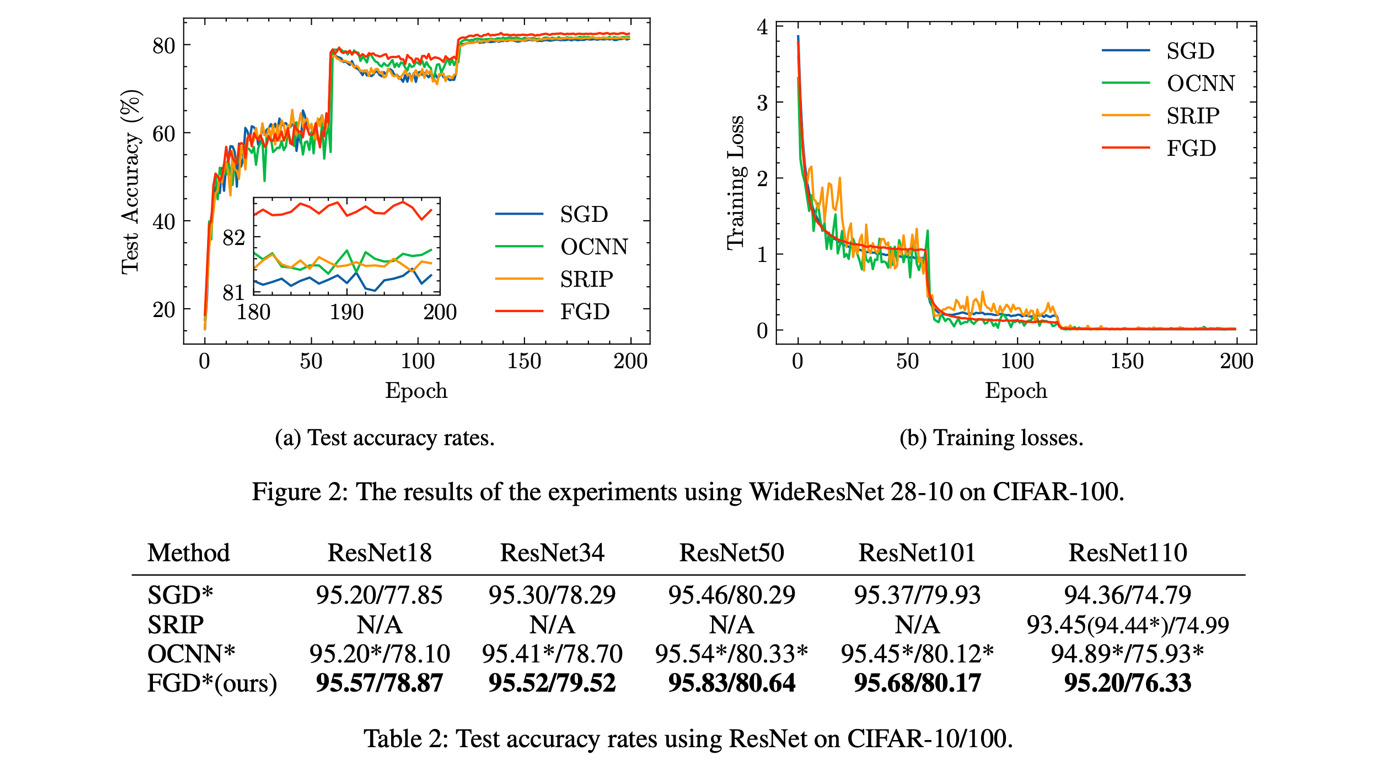
The optimization with orthogonality has been shown useful in training deep neural networks (DNNs). To impose orthog- onality on DNNs, both computational efficiency and stability are important. However, existing methods utilizing Rieman- nian optimization or hard constraints can only ensure stabil- ity while those using soft constraints can only improve ef- ficiency. In this paper, we propose a novel method, named Feedback Gradient Descent (FGD), to our knowledge, the first work showing high efficiency and stability simultane- ously. FGD induces orthogonality based on the simple yet indispensable Euler discretization of a continuous-time dy- namical system on the tangent bundle of the Stiefel manifold. In particular, inspired by a numerical integration method on manifolds called Feedback Integrators, we propose to instan- tiate it on the tangent bundle of the Stiefel manifold for the first time. In the extensive image classification experiments, FGD comprehensively outperforms the existing state-of-the- art methods in terms of accuracy, efficiency, and stability.